参考课程为自哈尔滨工业大学的 《编译原理》,参考教材为《编译原理及实践教程》(第三版)。
本文划分仅考虑本人每日复习量,没有章节划分参考价值。
文法的定义(Grammer)
文法是描述语言的语法结构的形式规则(即语法规则)。
以自然语言为例:
<句子> $\rightarrow$ <名词短语><动词短语>
<名词短语> $\rightarrow$ <形容词> <名词短语>
- <名词短语> $\rightarrow$ <名词>
<动词短语> $\rightarrow$ <动词> <名词短语>
<形容词> $\rightarrow$ little
- <名词> $\rightarrow$ boy
- <名词> $\rightarrow$ apple
- <动词> $\rightarrow$ eat
用尖括号括起来的的符号,是非终结符,他们不会出现在最终的句子当中。出现在最终的句子符号是终结符,他们由不带尖括号的符号。
产生式:按照一定规则书写的、用于定义语法范畴的规则,说明了终结符和非终结符组成符号串的方式。形如$a\rightarrow b$,其中$a$为左部,$a\in V^+$,且至少包含一个非终结符。$b$为右部,$b\in V^*$。
文法的形式化定义
$G = (V_T, V_N,P,S)$
$V_T$:终结符集合
$V_N$:非终结符集合
$P$:产生式集合
$S$:开始符号,表示该文法中最大的语法成分。
约定:在不引起歧义的前提下,可以只写文法的产生式。
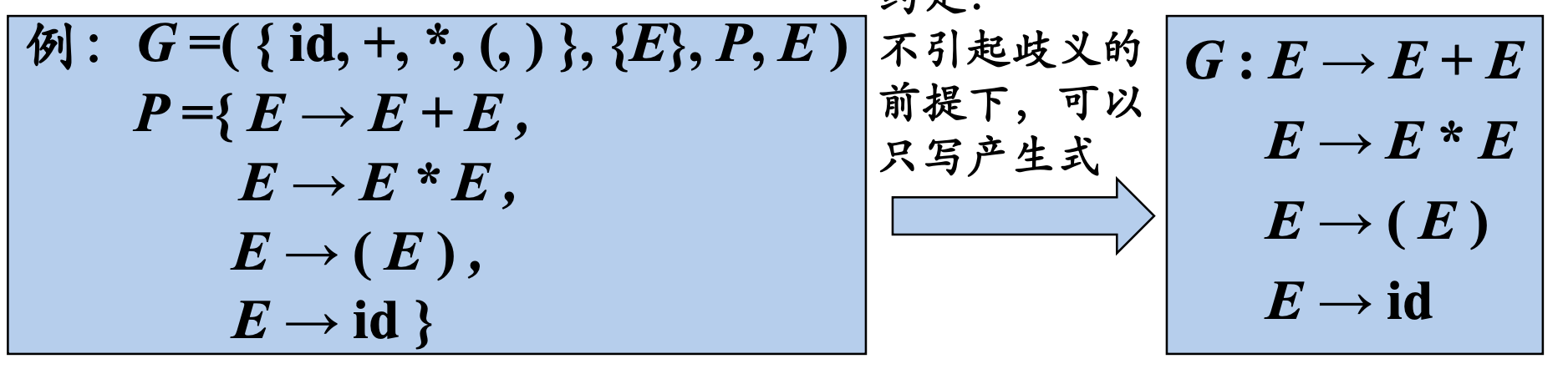
产生式的简写
对一组有相同左部的$\alpha$产生式 $\alpha\rightarrow \beta_1, \alpha\rightarrow \beta_n, \dots, \alpha\rightarrow \beta_n$
可以简写为: $\alpha\rightarrow \beta_1| \beta_2|\dots | \beta_n$
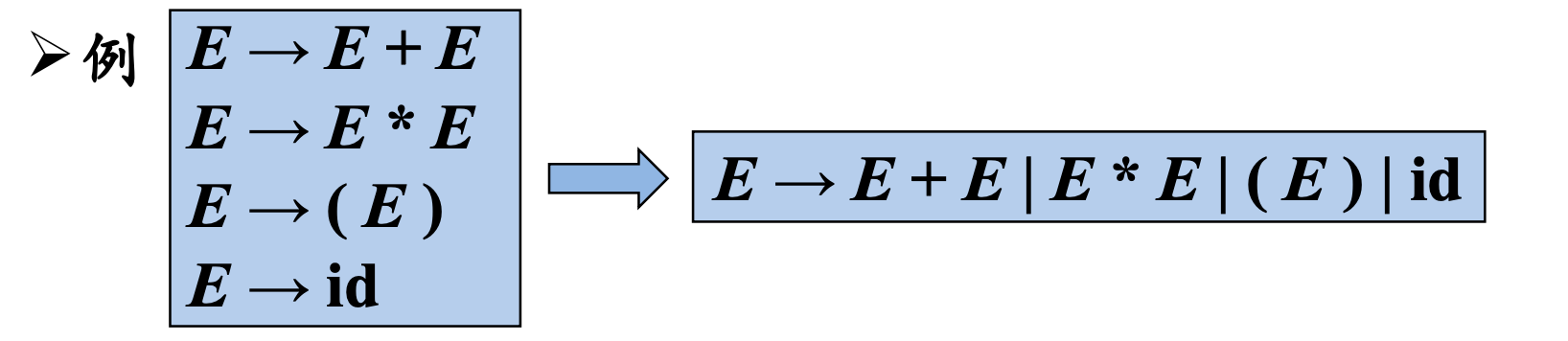
符号约定
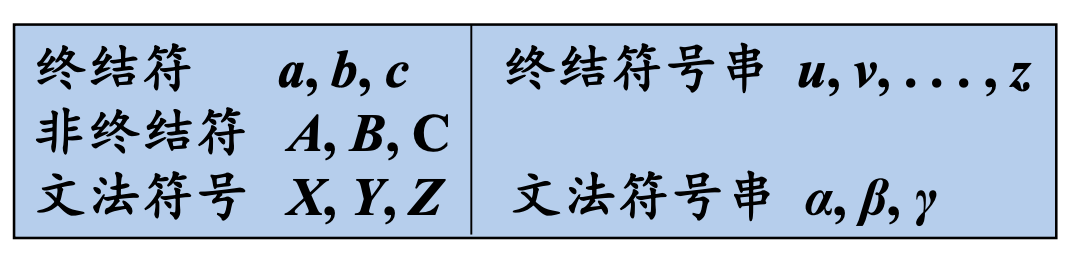
下述符号是终结符
- 字母表中排在前面的小写字母,如 a、b、c
- 运算符,如 +、 *等
- 标点符号,如括号、逗号等
- 数字0、1、. . . 、9
- 粗体字符串,如id、if等
下述符号是非终结符
- 字母表中排在前面的大写字母,如A、B、 C
- 字母S。通常表示开始符号
- 小写、斜体的名字,如 expr、stmt等
- 代表程序构造的大写字母。如E(表达式)、T(项) 和F(因子)
- 字母表中排在后面的大写字母(如X、Y、Z) 表示文法符号(即终结符或非终结符)
- 字母表中排在后面的小写字母(主要是u、v、. . . 、z) 表示终结符号串(包括空串)
- 小写希腊字母,如α、β、γ,表示文法符号串(包括空串)
- 除非特别说明,第一个产生式的左部就是开始符号
语言的定义
推倒和规约
给定文法$G = (V_T, V_N,P,S)$, 如果$\alpha\rightarrow\beta\in P$,那么可以将符号串$\gamma\alpha\delta$中的$α$替换为$β$,也就是说,将$γαδ$ 重写(rewrite)为$γβδ$,记作 $γαδ \rightarrow γβδ$。此时,称文法中的符号串$ γαδ $直接推导(directly derive)出 $γβδ$ 。
简而言之,就是用产生式的右部替换产生式的左部。
自顶向下分析(Top-Down Parsing)
从分析树的顶部(根节点)向底部(叶节点)方向构造分析树,可以看成是从文法的开始符号$S$推倒出词串$w$的过程。
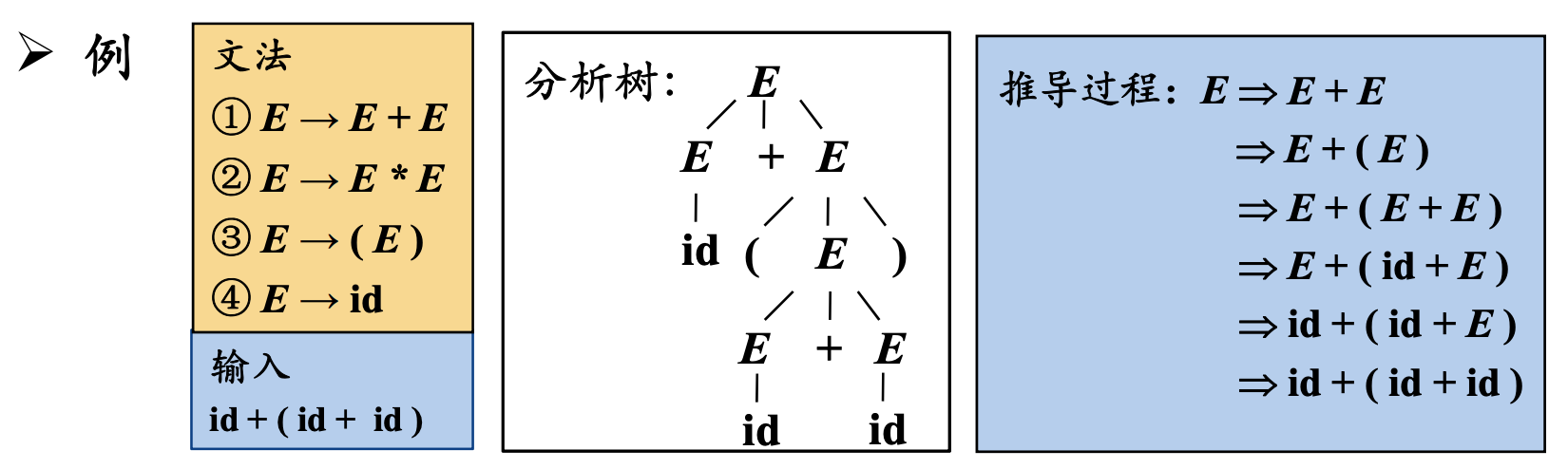
每一步推倒中都要做出两个选择:
- 替换当前句型中的哪个非终结符
- 用该非终结符的哪个候选式进行替换
最左推倒(Left-most Derivation)
在最左推倒中,总是选择每个句型的最左非终结符进行替换
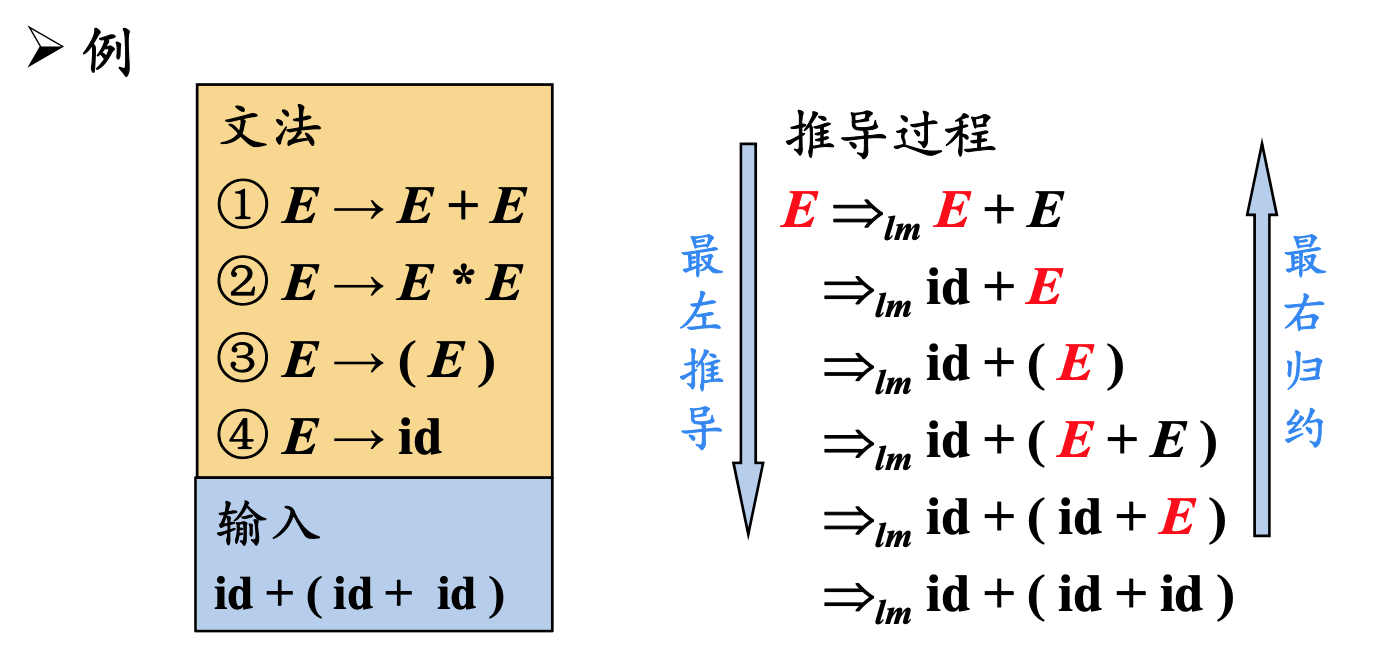
最右规约是最左推倒的逆过程。
如果$S\Rightarrow^{} _{lm}a$,则称$a$是当前文法的*最左句型
最右推倒(Right-most Derivation)
在最右推倒中,总是选择每个句型的最右非终结符进行替换
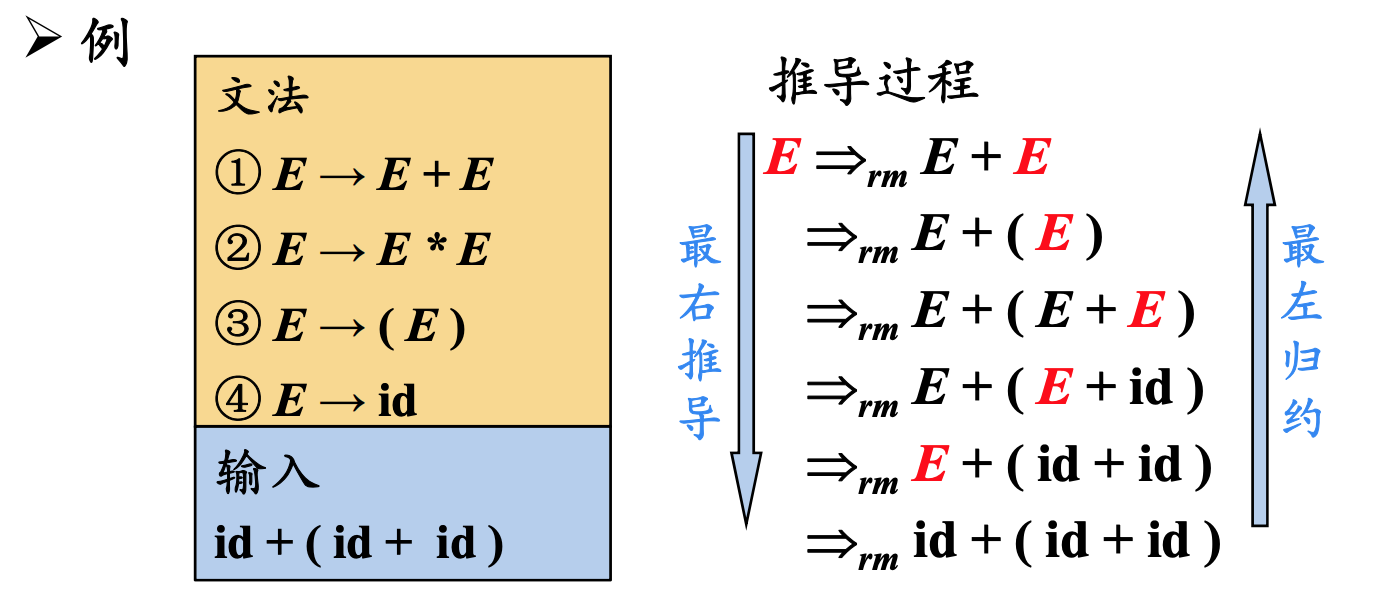
在自底向上的分析中,总是采用最左归约的方式,因此把最左归约称为规范归约,而最右推导相应地称为规范推导
最左推倒和最右推倒的唯一性
给定一棵分析树,在推倒的过程中可以选择任意一个非终结符进行替换。但是最左推倒和最右推倒是唯一的,因为最左/右非终结符是唯一的。
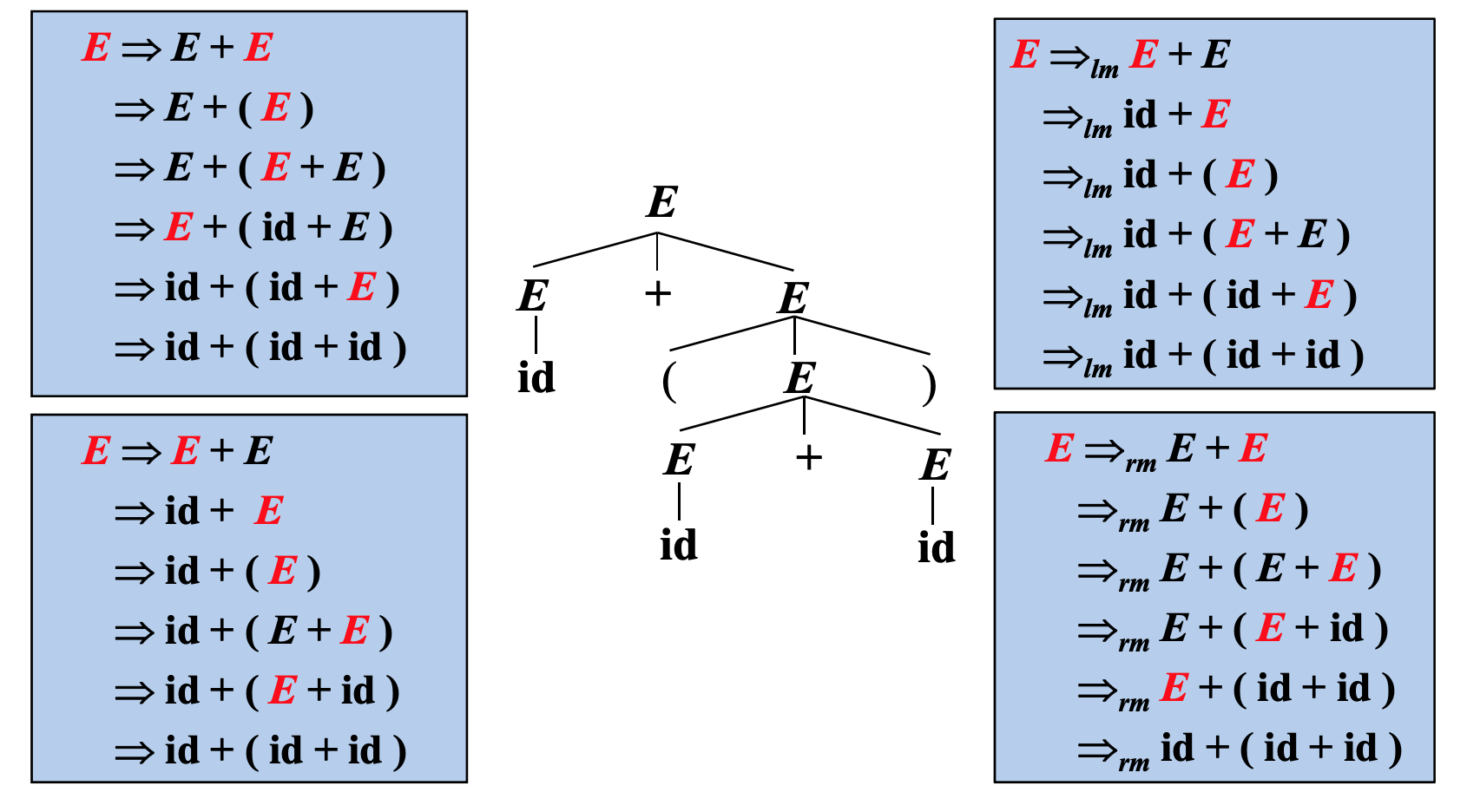
自顶向下的语法分析采用最左推导方式,总是选择每个句型的最左非终结符进行替换。根据输入流中的下一个终结符,选择最左非终结符的一个候选式。
文法转换
并不是所有的文法都适合自顶向下的分析, 例如
问题1 回溯
文法G
$S \rightarrow aAd|aBe$
$A\rightarrow c$
$B\rightarrow e$
输入: $a\ b\ c $
输入从$a$开始,而$S$的两个候选式都是以$a$开头的,导致回溯现象。
问题2 左递归
文法G
$E \rightarrow E+T|E-T|T$
$T \rightarrow T*F|T/F|F$
$F \rightarrow (E)|id$
输入:id + id * id
输入从id开始,需要逐个尝试,陷入$E \rightarrow\ E+T$递归。
含有 $A\rightarrow Aα$形式产生式的文法称为是直接左递 的 (immediate left recursive )
如果一个文法中有一个非终结符$A$使得对某个串 $α$ 存 在一个推导$A \Rightarrow ^+Aα$ ,那么这个文法就是左递归的
经过两步或两步以上推导产生的左递归称为是间接左递归的。
消除直接左递归
直接用$A\rightarrow A\alpha|\beta$推倒出来的式子代换即可。
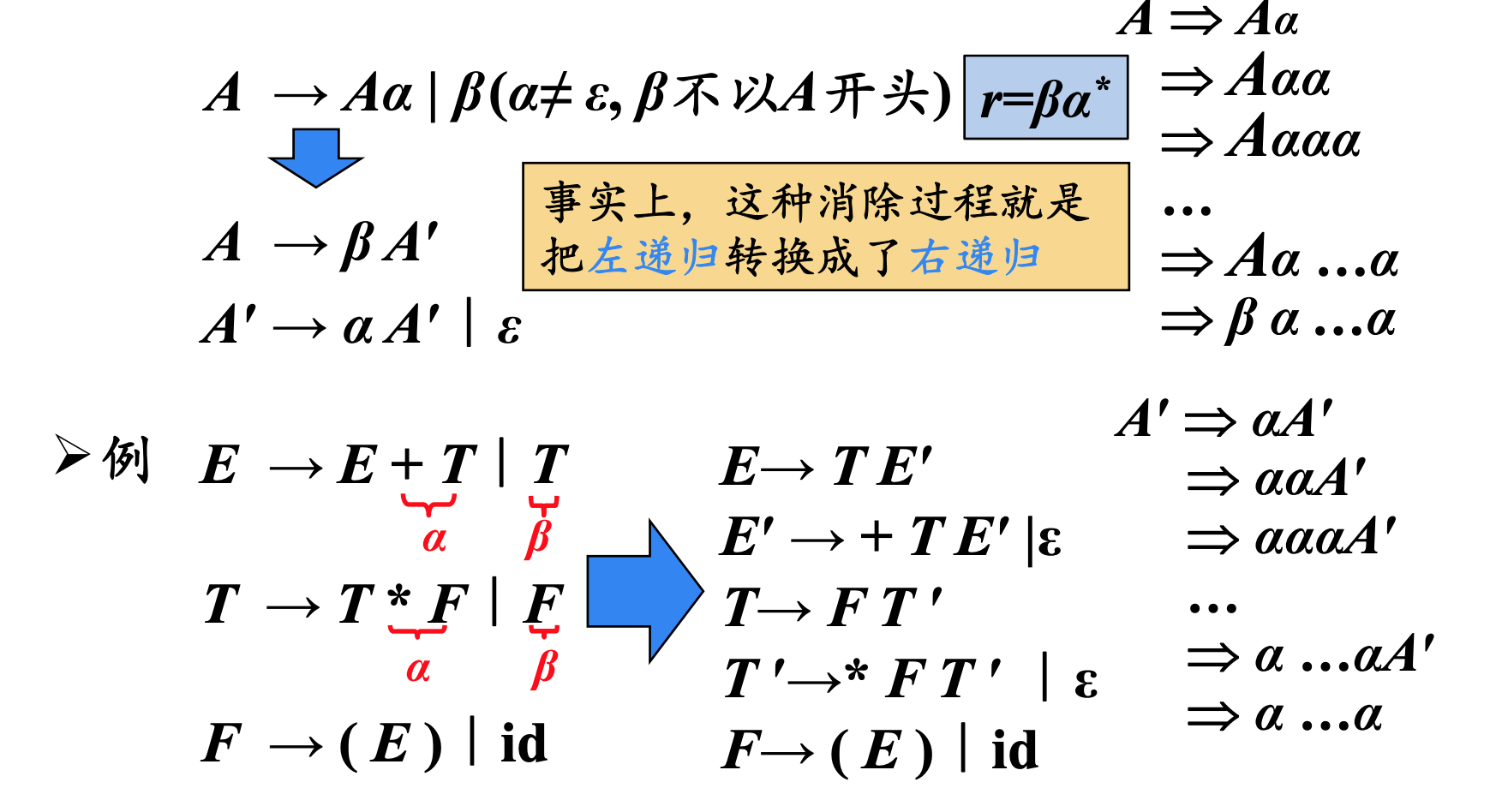
消除左递归付出的代价:引进引进了一些非终结符和$ε$产生式
消除间接左递归
用代入法转换成直接左递归消除。

回溯问题的解决——提取左公因子
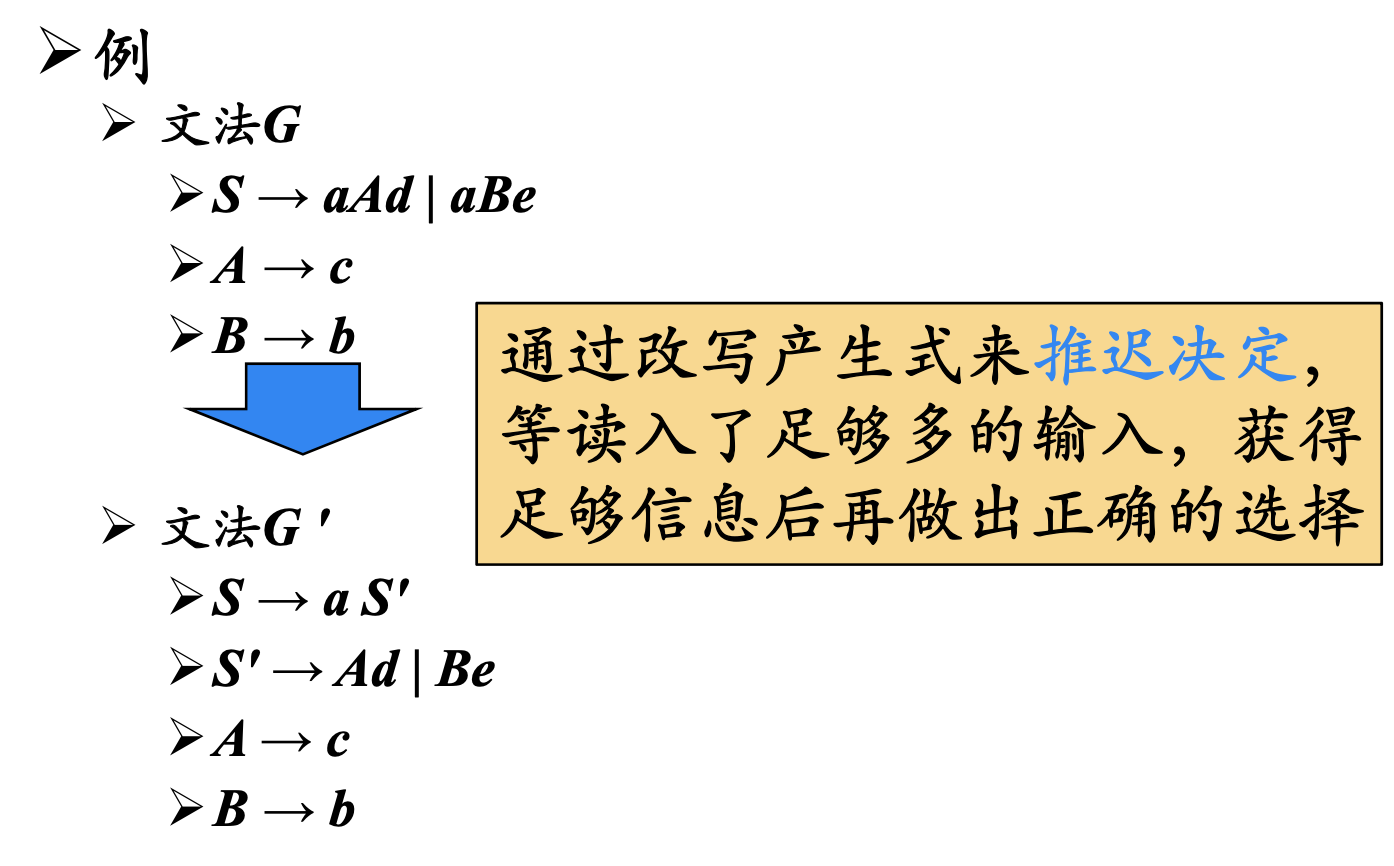
LL(1)文法
串首终结符集(FIRST集)
串首终结符:串首第一个符号,并且是终结符。简称首终结符。
给定一个文法符号串$α$, $α$的串首终结符集$FIRST(α)$被定义可以从$α$推导出的所有串首终结符构成的集合。如果$α \Rightarrow^* ε$, 那么$ε\in FIRST(α)$中。
符号的FIRST集的计算
- 把首终结符和空串加入到FIRST集中
- 若产生式右部以非终结符打头,那么这个非终结符的FIRST集中的所有终结符,都是产生式左边非终结符能推倒出的首终结符。

串的FIRST集的计算
- 向$FIRST(X_1,X_2,\dots,X_n)$加入$FIRST(X_1)$中的所有非$ε$符号。
- 如果$ε \in FIRST(X_1)$,再加入$FIRST(X_2)$中的所有非$ε$符号,以此类推。
- 如果对于所有的$i$,$ε$都在$FIRST(X_i)$中,那么将$ε$加入到$FIRST(X_1,X_2,\dots,X_n)$中。
FOLLOW集的计算
$FOLLOW(A)$:可能在某个句型中紧跟在$A$后面的终结符的集合。
- 将结束符$#$加入到$FOLLOW(S)$中,S为开始符号。
- 如果存在产生式$A\rightarrow \alpha B\beta$,那么$FIRST(\beta)$中的除了$ε$之外的所有符号都在$FOLLOW(B)$中。
- 如果存在一个产生式$A\rightarrow \alpha B$,或存在产生式$A\rightarrow \alpha B\beta$,且$FIRST(\beta)$包含$ε$,那么$FOLLOW(A)$中的所有符号都在$FOLLOW(B)$中。
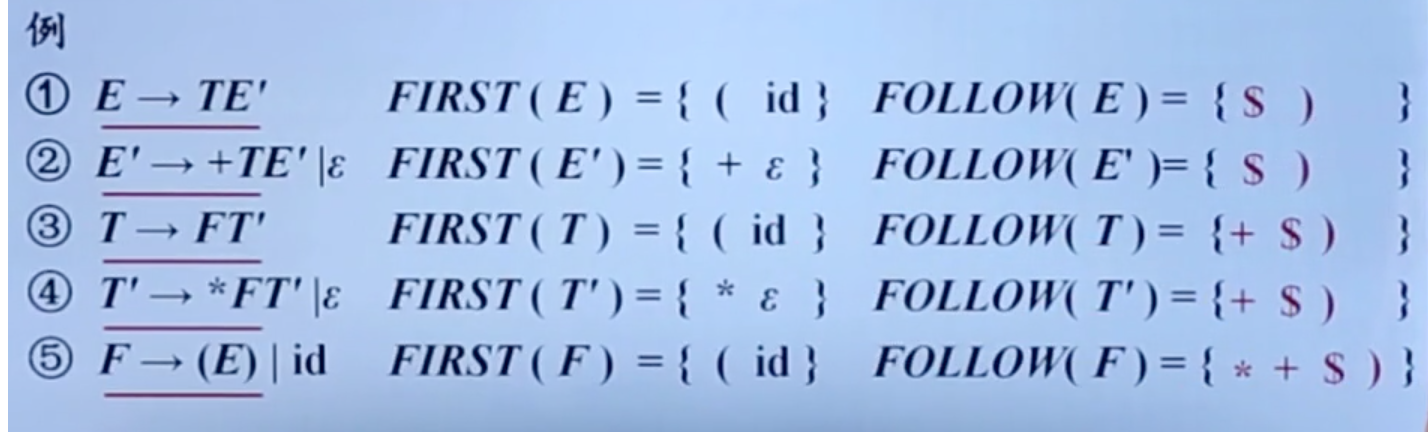
LL(1)文法
若文法$G$是LL(1)的,当且仅当G的任意两个具有相同左部的产生式A → α | β 满足下面的条件:
- 不存在终结符a使得α 和β都能够推导出以a开头的串
- $α$和$β$至多有一个能推导出$ε$如果 $β \Rightarrow^*ε$,则$FIRST (α)∩FOLLOW(A) = Φ$;
- 如果$α \Rightarrow^*\ ε$,则$FIRST (β)∩FOLLOW(A) =Φ$;



