参考课程为自哈尔滨工业大学的 《编译原理》,参考教材为《编译原理及实践教程》(第三版)。
本文划分仅考虑本人每日复习量,没有章节划分参考价值。
字母表
字母表$\Sigma$十一个有穷符号集合。 (符号包括字母、数字、标点符号)
二进制字母表$\{0,1\}$,ASCII字符集,Unicode字符集都属于字母表。
字母表的运算
- 乘积: $\Sigma_1\Sigma_2=\{a,b|a\in\Sigma_1, b\in\Sigma_2\}$ Ex: $\{0,1\}\{a,b\}=\{0a,0b,1a,1b\}$
幂:$\begin{equation}\left\{\begin{array}{lr}\Sigma^0 = \{\epsilon\}(空串) & \\ \Sigma^n=\Sigma^{n-1}\Sigma\end{array}\right.\end{equation}$ Ex: $\{0,1\}^3 = \{000,001,010,011,100,101,110,111\}$
正闭包:$\Sigma^+=\Sigma\bigcup\Sigma^2\bigcup\Sigma^3\bigcup\dots$ Ex: $\{a,b,c,d\}^+=\{a,b,c,d,aa,ab,ac,ad,ba,bb,bc,bd,ca,cb,cc,cd,da,db,dc,dd,aaa,\dots\}$
(克林)闭包:$\Sigma^*=\Sigma^0\bigcup\Sigma^+$ 就是在正闭包的基础上加上一个空串。
串
设$\Sigma$是一个字母表,$\forall{x\in\Sigma^*}$,称$x$为$\Sigma$上的一个串,串是字母表中符号的一个有穷序列。
串$s$的长度通常记为$|s|$,指$s$中符号的个数。 Ex: $|aab|=3$
串上的运算
连接:$xy$ , $x=dog, y=house, xy=doghouse$
对于空串:$\epsilon s=s\epsilon = s$
设$x,y,z$是三个字符串,若$x = yz$,则$y$为$x$的前缀,$z$为$x$的后缀。
幂运算:$\begin{equation}\left\{\begin{array}{lr}s^0 = \epsilon, & \\ s^n=s^{n-1}s, &n\geq1\end{array}\right.\end{equation}$ Ex: $s=ba,s^1=ba,s^2=baba,s^3=bababa$
正则表达式(RE)
语言可以用集合表示,设语言
正则表达式是一种用来描述正则语言的更紧凑的表示方法。
例如
正则表达式可以由较小的正则表达式按照特定规则递归的构建。每个正则表达式$r$定义(表示)一个语言,记为$L(r)$。这个语言是根据$r$的字表达式递归定义的。
正则表达式的定义
- $\epsilon$是一个RE,$L(\epsilon) = \epsilon$
- 如果$a\in\Sigma$,则$a$是一个RE,$L(a) = \{a\}$
- 假设$r$和$s$都是RE,表示的语言分别为$L(r)$和$L(s)$,则:
- $r|s$是一个RE,$L(r|s)=L(r)\bigcup L(s)$
- $rs$是一个RE,L(rs) = L(r)L(s)$
- $r^$是一个RE,L(r^)=L(r)^*$
- $(r)$是一个RE,L((r))=L(r)$
运算优先级: $* > $ 连接 $> |$
正则定义
正则定义就相当于一个函数封装。
有穷自动机(FA)
转换图
初始状态用$\Rightarrow$表示, 终止状态用双圈表示。
由一个有穷自动机$M$接收的所有串构成的集合称为是FA定义(或接收)的语言,记为$L(M)$。

最长字串匹配原则
当输入串的多个前缀与一个或者多个模式匹配时,总是选择最长的前缀进行匹配。
说人话就是到了终止状态,若还有符号,则继续前进。
确定的有穷自动机(DFA)
$S$:有穷状态集
$\Sigma$:输入字母表
$\delta$:将$S\times\Sigma$映射到$S$的转换函数,$\delta(s,a)$表示从s出发,沿a能到达的状态
$s_0$:开始状态(或初始状态),$s_0\in S$
$F$:接收状态(或终止状态)集合,$F\subseteq S$
DFA也可以用转换表来表示
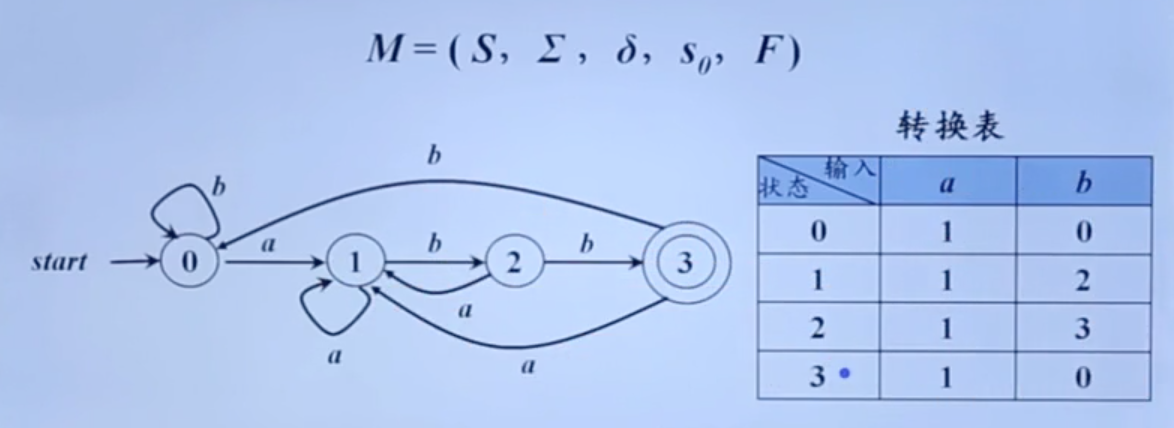
不确定的有穷自动机
和DFA的区别在于,$\delta(s,a)$表示从s出发,沿a能到达的所有状态的集合。
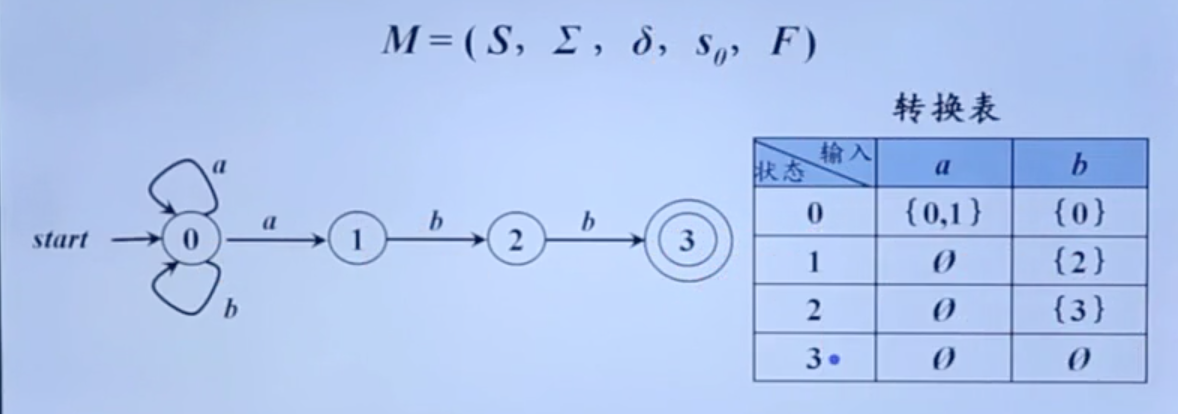
NFA和DFA的等价性
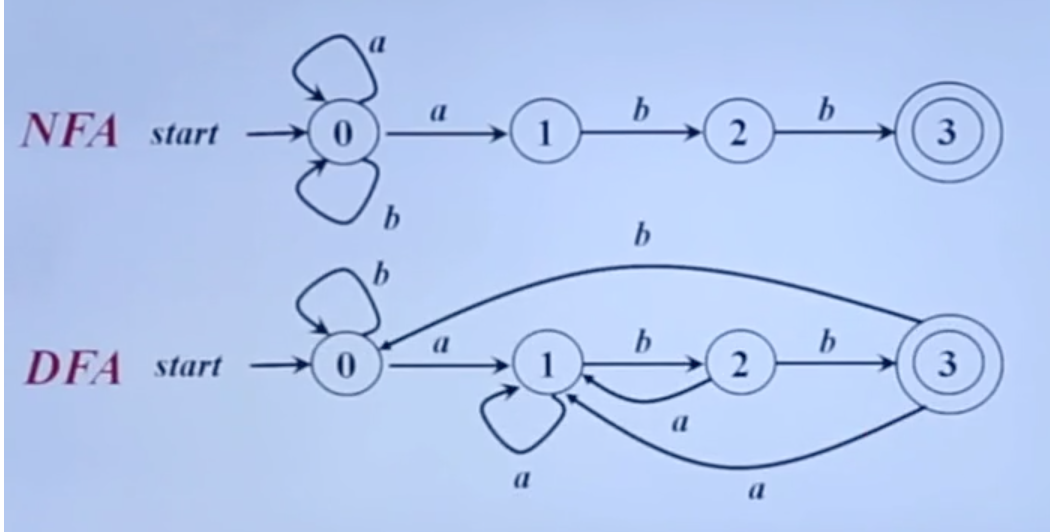
在上图的DFA中,状态1表示串以a结尾,状态2表示串以ab结尾,状态3表示串以abb结尾。
他们都是$r=(a|b)^*abb$,由此$RE \Leftrightarrow FA \Leftrightarrow 正则文法$。
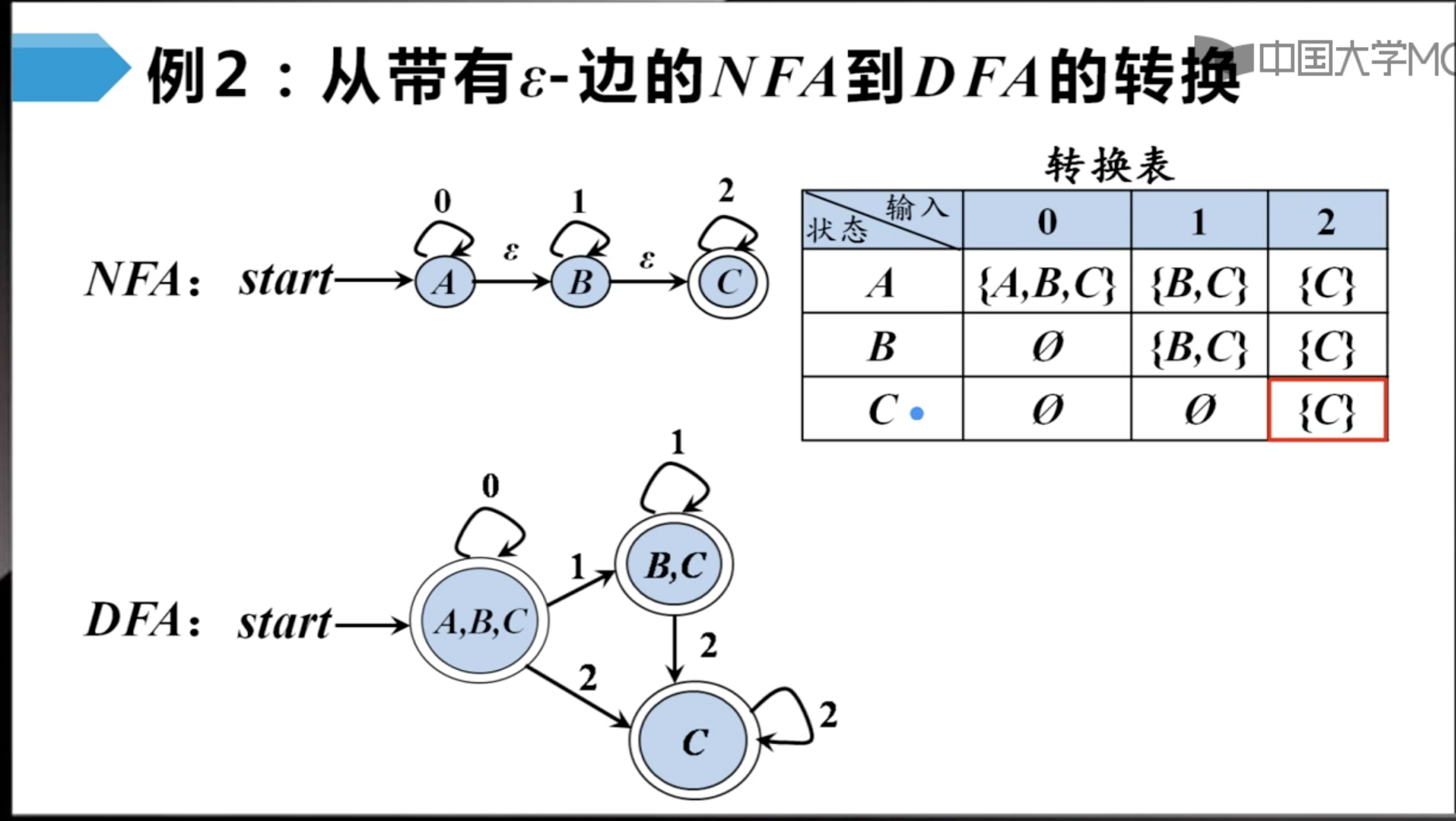
带有和不带有$\epsilon$边的NFA的等价性
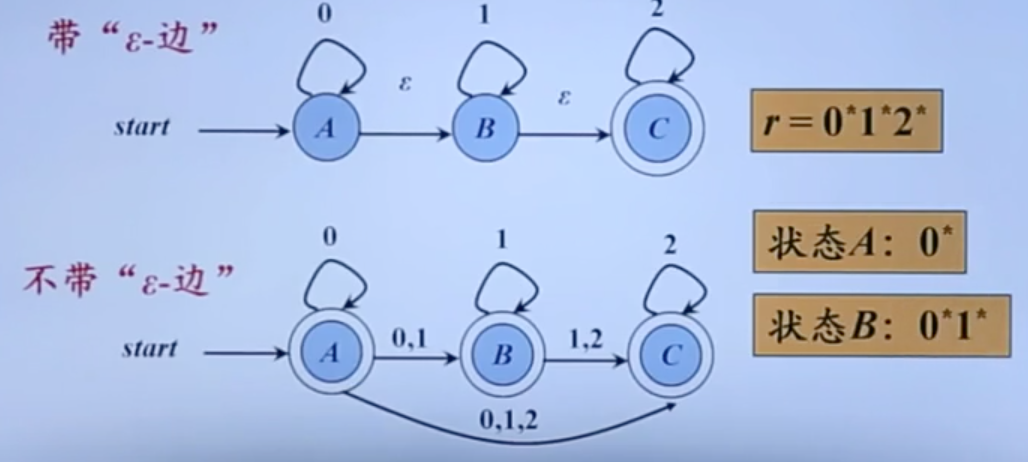
从正则表达式到有穷自动机
根据RE构造NFA

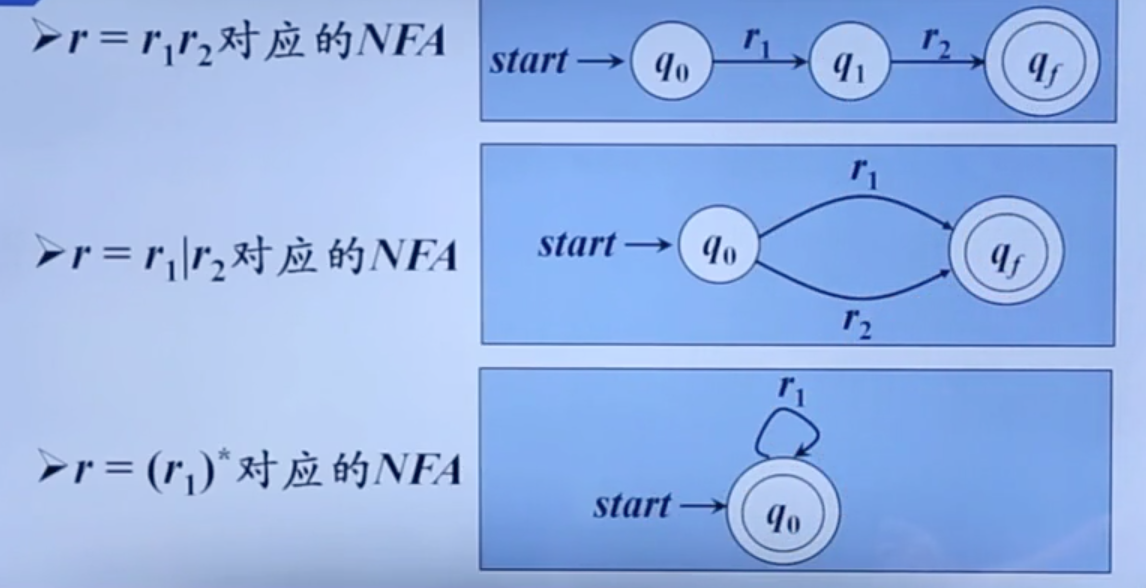
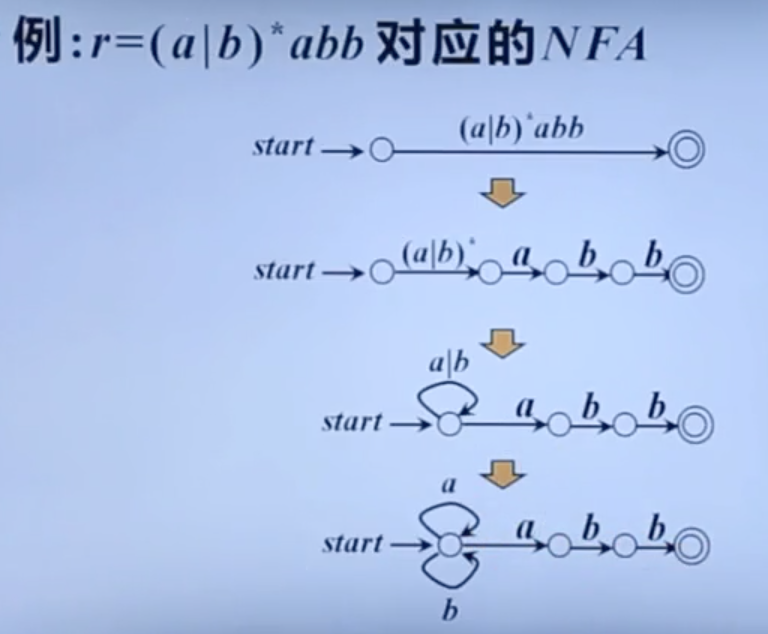
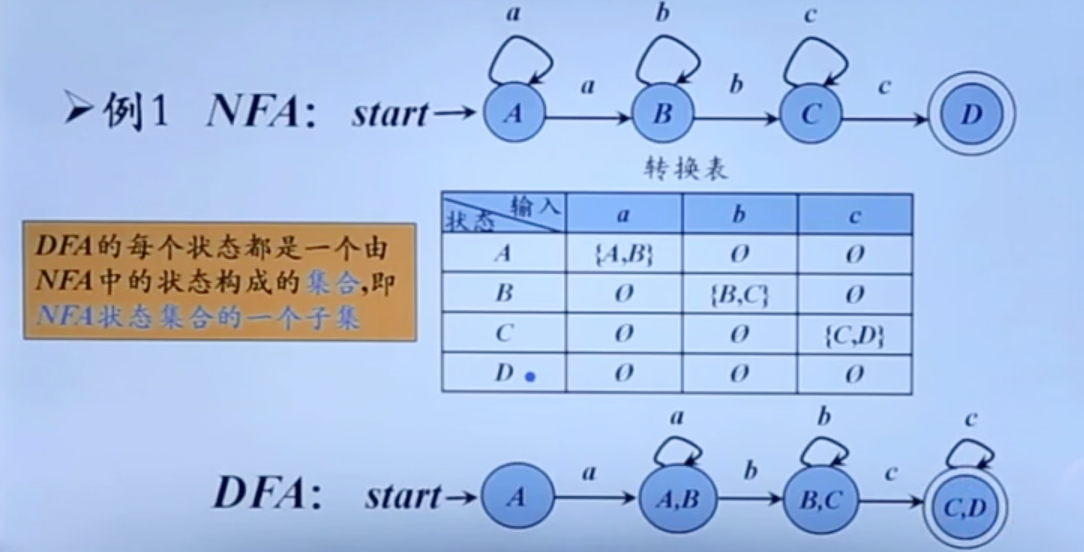
从NFA到DFA的转换
子集构造法。