参考课程为自哈尔滨工业大学的 《编译原理》,参考教材为《编译原理及实践教程》(第三版)。
本文划分仅考虑本人每日复习量,没有章节划分参考价值。
CFG的分析树
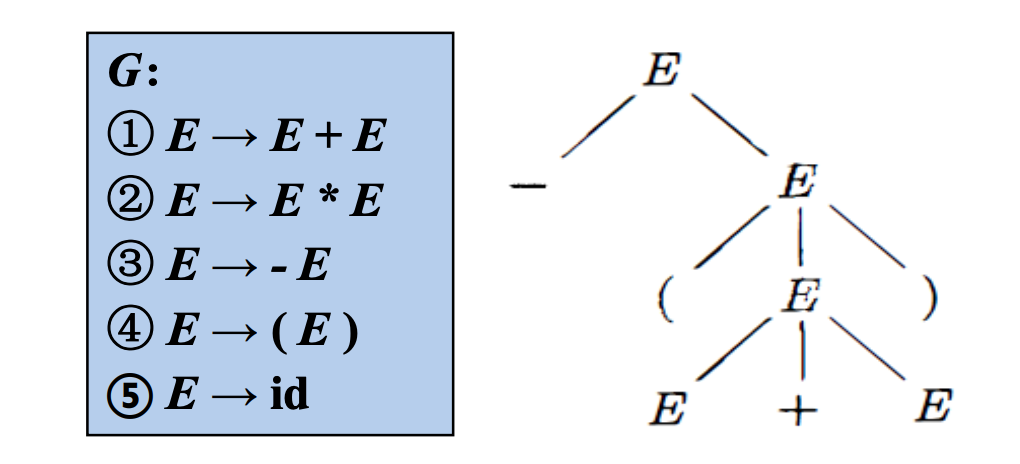
根节点对应文法开始符号。
内部节点表示对一个产生式的应用,该节点的标号是此产生式的左部。该节点的子节点的标号从左到右构成了产生式的右部。
叶节点的标号既可以是非终结符,也可以是终结符。从左到右排列叶节点得到的符号串称为这棵树的产出或者边缘。
分析树是推导的图形化表示
给定一个推导$S\Rightarrow a_1\Rightarrow a_2 \Rightarrow \dots \Rightarrow a_n$,对于推导过程中的每一个句型$a_i$,都可以构造出一个边缘为$a_i$的分析树。
(句型的)短语
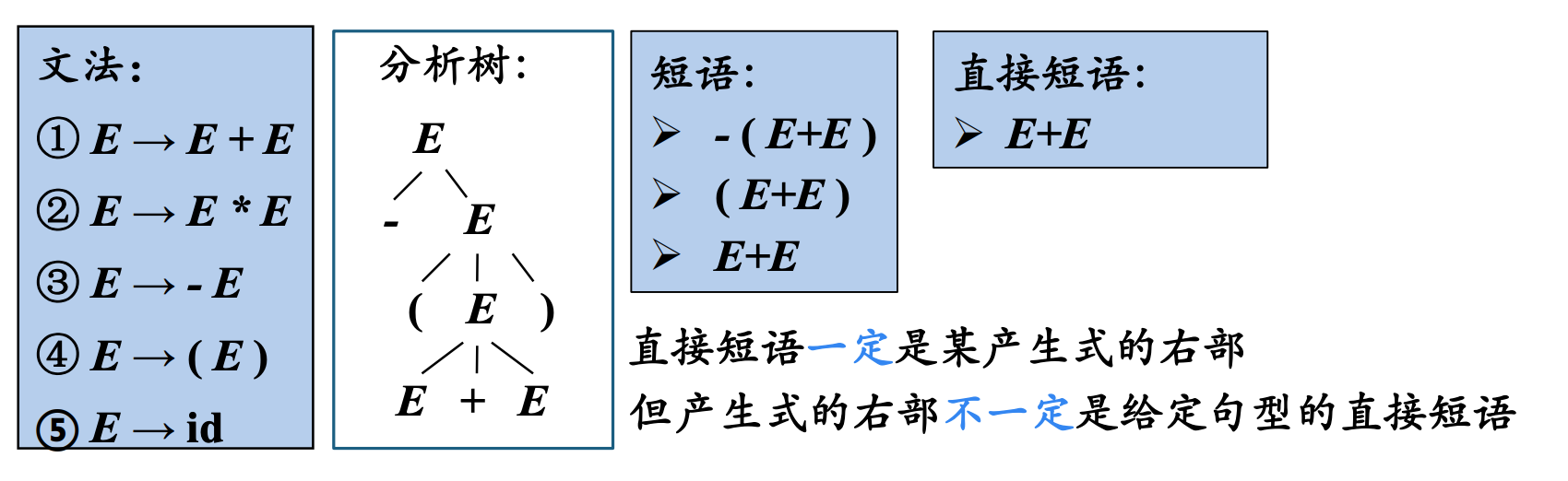
给定一个句型,其分析树中的每一棵子树的边缘称为该句型的短语。
如果子树只有父子两代节点,那么这棵子树的边缘称为该句型的一个直接短语。
自底向上的语法分析
从分析树的底部(叶节点)向顶部(根节点)方向构造分析树。可以看成是输入串$w$规约为文法开始符号$S$的过程。
自底向上的语法分析采用最左规约方式(反向构造最右推导)。自底向上语法分析的通用框架是移入-规约分析。
移入-规约分析
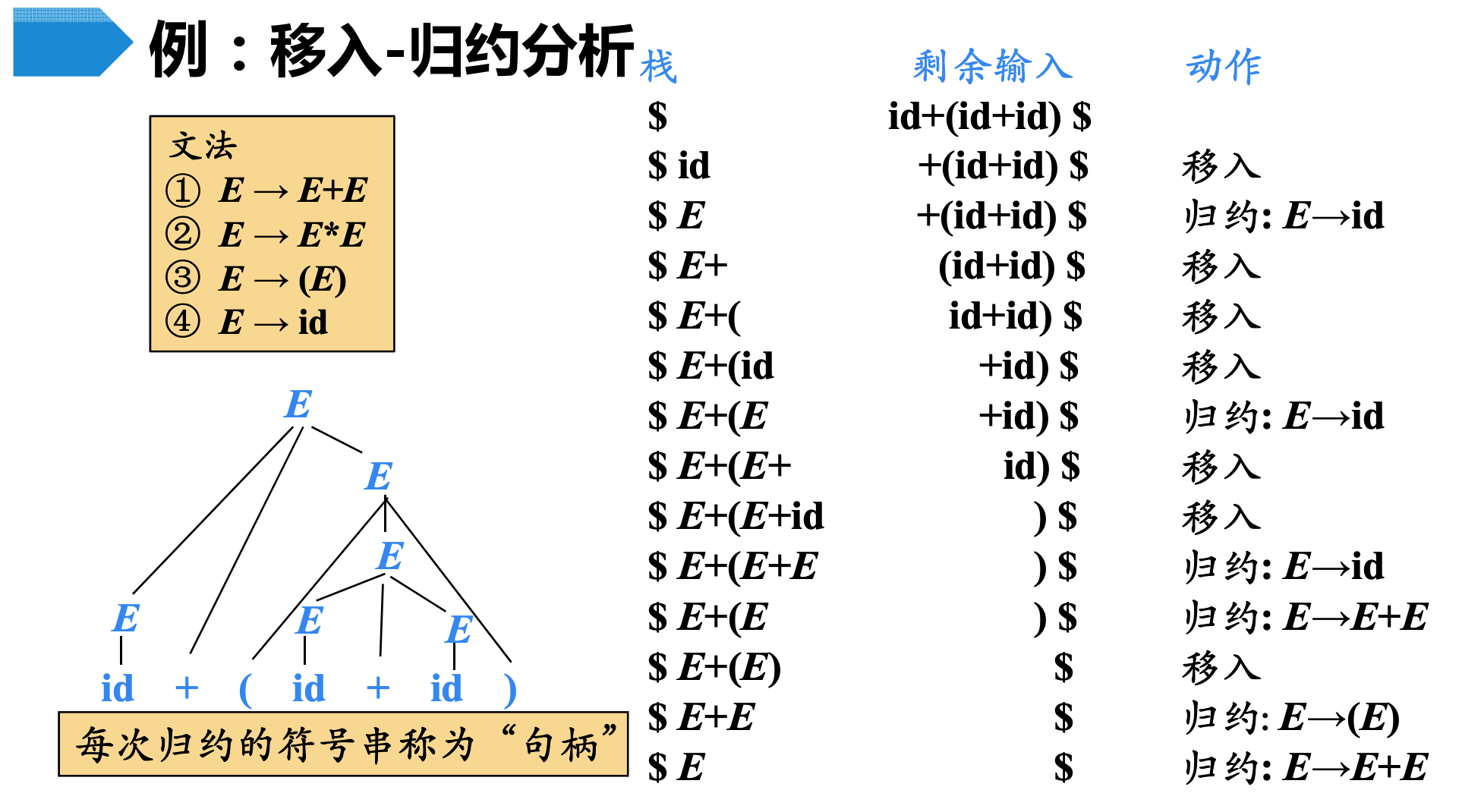
- 每次规约的符号串称为句柄。
- 站内符号串+剩余输入=规范句型
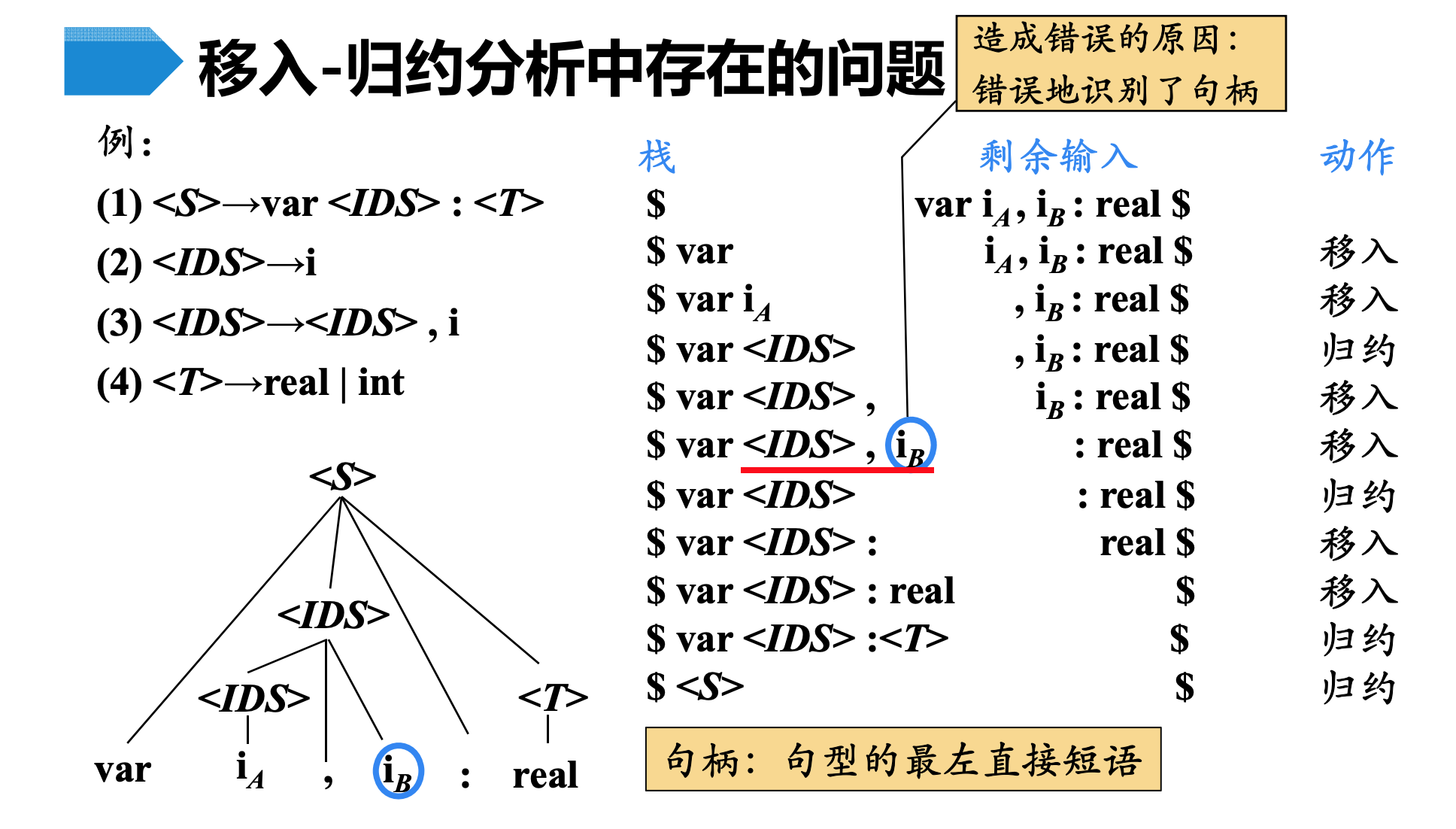
移入-规约分析中存在的问题
句型实际上是当前句型的最左直接短语。
算符优先分析
算符文法
一个文法,如果它的任何产生式的右部都不含两个相继(并列)的非终结符结构,即不含如下形式的产生式:
则称该文法是算符文法。
假定$G$是不含$ε$产生式的算符文法,终结符对a、b之间的优先关系定义如下。
- $a \dot= b$当且仅当文法G中含有形如$P \rightarrow ab$或者$P \rightarrow aQb$的产生式。
- $a \dot< b$当且仅当文法G中含有形如$P \rightarrow aR$的产生式,且$R\Rightarrow^+b\dots$或$R\Rightarrow^+Qb\dots$。
- $a \dot> b$当且仅当文法G中含有形如$P \rightarrow Rb$的产生式,且$R\Rightarrow^+a\dots$或$R\Rightarrow^+aQ\dots$。
算符优先文法:若G是一个不含空产生式的算符文法,任何终结符对(a, b)只满足下述三种优先关系之一:
则称G为一个算符优先文法,简称OPG文法。算符优先文法是无二义性的。
算符优先表
FirstVT和LastVT集
对于文法G的任一非终结符P,定义两个集合:
FirstVT(P):P能推倒的第一个终结符构成的集合。
LastVT(P):P能推导的最后一个终结符构成的集合。
算符优先表的构造
- $\dot=$关系:若有形如$P \rightarrow \dots ab\dots$或$P \rightarrow \dots aQb\dots$的产生式,则$a\dot= b$。可以直接看产生式得到。
- $\dot<$关系:若有形如$Q\rightarrow\dots aP\dots$的产生式,对任何$b\in FirstVT(P)$,有$a\dot<b$。
- $\dot>$关系:若有形如$Q\rightarrow\dots Pb\dots$的产生式,对任何$a\in LastVT(P)$,有$a\dot>b$。
算符优先分析过程
和移进-规约过程基本相同。只是在满足$\dot<$或者$\dot=$时移入,在$\dot>$时规约。
算符优先分析中,句型可以用一般形式(N)表示,在规约过程中,只需终结符相同,非终结符位置相同即可。
LR分析法
LR文法
可以运用LR分析法的文法称为LR文法。LR文法是最大的、可以构造出相应移入-规约语法分析器的文法类。
- L:对输入进行从左到右的扫描
- R:反向构造出一个最右推导序列
LR(k)分析:需要向前查看k个输入符号的LR分析。当k=0和k=1这两种情况时具有实际意义。当省略(k)时,表示k=1。
LR分析法的基本原理
句柄是逐步形成的,用“状态”表示句柄识别的进展程度。

LR分析器(自动机)的总体结构
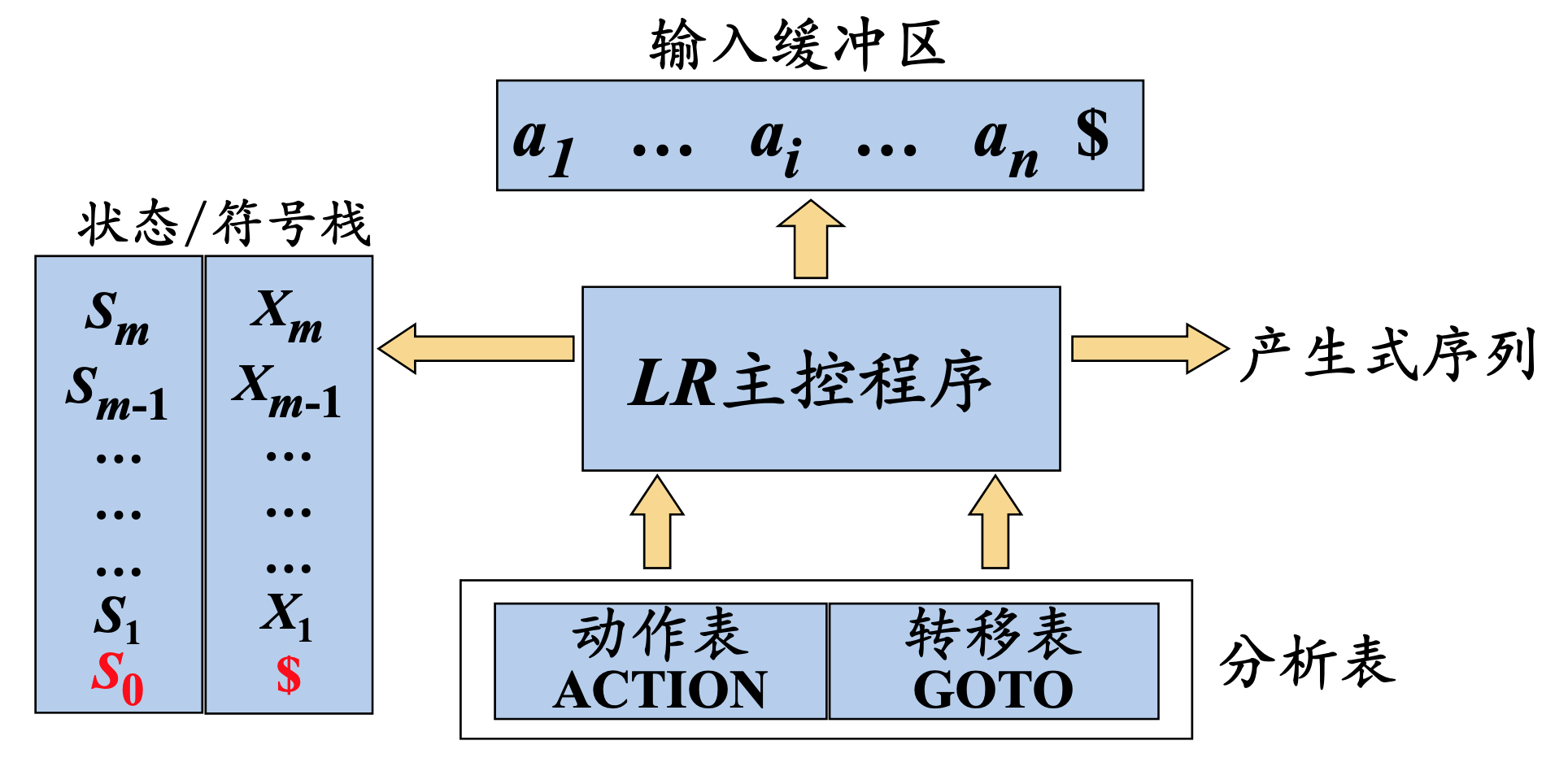
Ex: 文法$S\rightarrow BB \\ B\rightarrow aB \\ B\rightarrow b$对应的LR分析表为:

在上表中,每一行对应一个状态,一共有7个状态;Action表中的每一列分别对应文法中的终结符,以及结束符号#;Action表中的每一项表示对应的语法分析动作,sn表示将当前符号移入到分析栈中,并且进入状态n。rn表示用第n个产生式进行规约;GOTO表的每一列对应着文法中的非终结符;GOTO表中的每一项表示在某一状态遇到某一非终结符遇到的后继状态。
假设输入为b a b,则会有以下的分析过程:








